Triángulo de Impedancia: Desentrañando el Corazón de la Electricidad
En el fascinante mundo de la electricidad, cada componente juega un papel crucial en el funcionamiento de circuitos y sistemas. Entre los conceptos más intrigantes, el triángulo de impedancia se destaca como una herramienta esencial para entender la relación entre la resistencia, la reactancia y la impedancia. Pero, ¿qué significa realmente esta figura geométrica en el contexto eléctrico? ¿Cómo influye en el rendimiento de nuestros dispositivos y en la eficiencia energética? En este artículo, exploraremos los fundamentos del triángulo de impedancia, revelando sus secretos y aplicaciones prácticas que pueden transformar nuestra comprensión del flujo eléctrico. ¡Prepárate para sumergirte en un viaje de descubrimiento que iluminará los aspectos más profundos de la electricidad!
¿Qué pasa cuando la electricidad y el magnetismo se encuentran? Esto es precisamente lo que exploraremos en este artículo sobre el Triángulo de Impedancia. Este concepto fundamental en el campo de la electricidad y la electrónica nos permite entender cómo interactúan estos dos fenómenos y cómo pueden afectar nuestras vidas en diferentes situaciones. ¿Estás listo para desenredar el misterio de la electricidad? ¡Acompáñanos y descubramos juntos el fascinante mundo del Triángulo de Impedancia!
Triángulo de impedancia es un triángulo rectángulo cuyos lados representan la impedancia. La base, la perpendicular y la hipotenusa representan la Resistencia, la Reactancia y la Impedancia respectivamente. es básicamente una representación geométrica de la impedancia del circuito.
Usando el triángulo de impedancia podemos encontrar la resistencia si se conocen la impedancia y la reactancia.
¿Qué es el triángulo de impedancia?
La impedancia (Z) consta de dos componentes
- Resistencia (R)
- Reactancia (X)
La resistencia atrae la potencia real o potencia activa porque el ángulo de fase entre el voltaje y la corriente es cero. La base del ángulo recto representa la potencia activa, y por lo tanto la base del triángulo representa la resistencia(R)
La reactancia (X) es el componente reactivo que extrae potencia reactiva. La potencia activa neta consumida por la reactancia es cero. En medio ciclo extrae la potencia reactiva y en otro medio ciclo vuelve a entregar potencia reactiva a la red eléctrica. El ángulo entre el voltaje y la corriente es de 90 grados y la potencia activa consumida por la potencia reactiva es cero.
Por lo tanto, podemos representar el componente reactivo (X) en el lado perpendicular del triángulo.
Desde arriba, está claro que la resistencia (R) y la reactancia (X) están a 90 grados entre sí en un triángulo de impedancia. La impedancia es la combinación de la resistencia (R) y la reactancia (X). Las unidades SI de resistencia, reactancia e impedancia son ohmios (Ω).
La impedancia (Z) se puede representar en el lado de la hipotenusa del triángulo. Por lo tanto, la impedancia (Z) es un número complejo. Representamos el número complejo como A+jB.
La oposición total que ofrece un circuito al flujo de un circuito de corriente alterna se denomina impedancia. La oposición es creada por los componentes del circuito R, L y C.
Z = R + j X
Representación de R,X y Z en el Triángulo de Impedancia
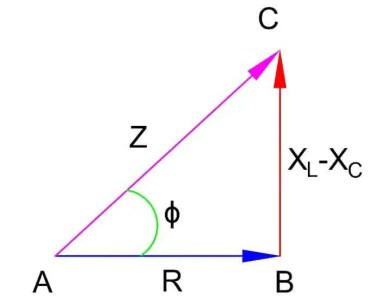
La representación geométrica de R, X y Z se muestra a continuación.
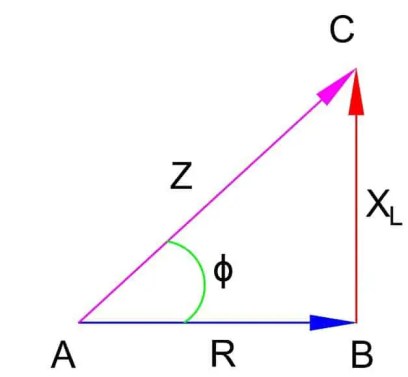>El triángulo ABC anterior se llama triángulo de impedancia. Aquí.
AB = Base del triángulo = R
BC = Perpendicular del triángulo = X
AC = hipotenusa del triángulo = Z
Si el circuito hacomponentes R, L y C, entonces el capacitor y el inductor ofrecen la reactancia. La reactancia del inductor está en oposición de fase con el capacitor y la reactancia neta en este caso es;
X = XL – XC
Dónde, XL y XC son dependientes de la frecuencia.
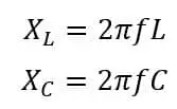>Relación entre R,L y C
Podemos establecer la relación entre R,X y Z usando el Teorema de Pitágoras para el triángulo de ángulo recto ABC.
C.A.2 = AB2 + BC2
Z2 = R2 +X2
Z = √ (R2 +X2 )
Triángulo de impedancia del circuito RL, RC y RLC
Impedancia del circuito RL
>
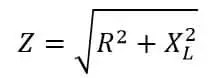Impedancia del circuito RC;
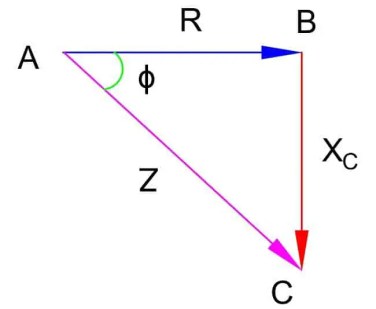>Impedancia del circuito RLC;
>
Leer más: Resistencia y reactancia de fuga del transformador
El ángulo entre la resistencia (R) y la impedancia (X)
bronceado ø = (X/R)
ø = bronceado-1(X/R)
Por lo tanto, usando el Triángulo de impedancia, podemos encontrar la magnitud y el ángulo de impedancia de un circuito.
Importancia del Triángulo de Impedancia
Podemos encontrar las siguientes cantidades eléctricas usando el triángulo de impedancia.
1. Cálculo de la impedancia
Podemos calcular la impedancia del circuito complejo, si tenemos los datos de cantidad conocida como resistencia (R) y reactancia (X).
Z = √ (R2 +X2 )
2. Cálculo del Factor de Potencia
cosø representa el factor de potencia del triángulo. En triángulo ABC,
Cosø = AB/ AC = R /Z
Cosø = R / Z
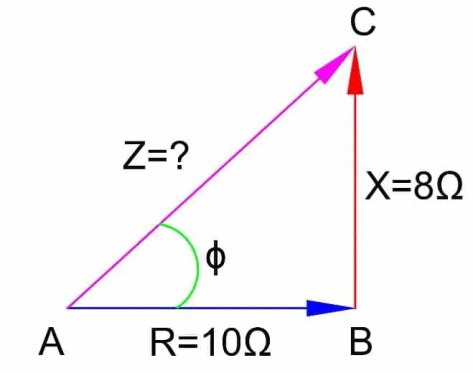
Sea la impedancia de un circuito Z = 10+j8. A partir de estos datos podemos calcular la impedancia y el factor de potencia del circuito.
>Z = √ (R2 +X2 )
Aquí, R = 10 Ω
X = 8 Ω
Z = √ (102 + 82 ) = √ (100 +64 ) = √ 164
= √ 164
Z = 12,8 Ω
La impedancia del circuito es de 12,8 Ω.
Factor de potencia
Cosø = R / Z = 10/12,8
Cosø = 0,781
Leer siguiente:
[automatic_youtube_gallery type=»search» search=»Triángulo de impedancia» limit=»1″]
Triángulo de Impedancia: Desentrañando el Corazón de la Electricidad
¿Qué es el triángulo de impedancia?
El triángulo de impedancia es una representación geométrica que ilustra la relación entre la resistencia (R), la reactancia (X) y la impedancia (Z) en un circuito eléctrico de corriente alterna.
Este triángulo es un triángulo rectángulo donde:
- Base: Representa la resistencia (R).
- Perpendicular: Representa la reactancia (X).
- Hipotenusa: Representa la impedancia (Z).
Componentes del triángulo de impedancia
La impedancia (Z) está compuesta por dos componentes fundamentales:
- Resistencia (R): Atrae potencia real o activa, donde el ángulo de fase entre el voltaje y la corriente es cero.
- Reactancia (X): Es el componente que extrae y entrega potencia reactiva al sistema, actuando como un almacenamiento de energía.
La fórmula general que describe la relación entre ellos es:
Z = R + jX
donde j es la unidad imaginaria.
Utilidad del triángulo de impedancia
Entender el triángulo de impedancia es crucial para analizar circuitos eléctricos, ya que permite calcular la resistencia si se conocen la impedancia y la reactancia. Este concepto es esencial para optimizar el rendimiento de dispositivos eléctricos y mejorar la eficiencia energética en diversas aplicaciones.
Preguntas Frecuentes (FAQs)
¿Por qué es importante la impedancia en un circuito eléctrico?
La impedancia se considera una medida crucial en circuitos eléctricos porque determina la oposición total que presenta un circuito al flujo de corriente alterna. Controlar la impedancia es esencial para el diseño y funcionamiento eficaz de los sistemas eléctricos, especialmente en aplicaciones de telecomunicaciones y electrónica de potencia.
¿Cómo se calcula la impedancia?
La impedancia se puede calcular utilizando la fórmula Z = √(R² + X²), donde R es la resistencia y X es la reactancia. Esto permite encontrar la magnitud de la impedancia y la fase del circuito.
¿Qué son la resistencia y la reactancia?
La resistencia es la oposición que presenta un conductor al paso de corriente continua, medida en ohmios (Ω). La reactancia, por otro lado, es la oposición ofrecida por componentes inductivos y capacitivos al flujo de corriente alterna, y también se mide en ohmios.
It seems like your request is incomplete. Could you please provide more details about what you would like me to write a single on? Are you looking for a single piece of writing, a song, a story, or something else? Let me know how I can assist you!
Constantin robert: ¡Totalmente de acuerdo, xamena! Yo también recuerdo mis días en la universidad lidiando con el triángulo de impedancia. Una vez, en un lab, casi me quedo atorado con un circuito que parecía un rompecabezas. Pero después de darle vueltas y entender cómo funciona la impedancia, todo cobró sentido. Es asombroso cómo un concepto tan abstracto puede tener aplicaciones tan prácticas. ¡Gran artículo!
¡Me encanta el artículo sobre el triángulo de impedancia! La verdad es que cuando estudié en la universidad, me volví un poco loco tratando de entender cómo aplicarlo en circuitos eléctricos. Una vez, hice un proyecto donde terminé usando esa fórmula y fue un lío, pero al final me di cuenta de lo útil que puede ser. ¡Gracias por resumirlo tan bien!
Aztiria: ¡Qué artículo tan interesante! A mí también me tomó su tiempo captar bien el triángulo de impedancia. Recuerdo que en un proyecto de electricidad me costó un mundo calcular la impedancia correcta para un circuito, pero una vez que lo logré, todo funcionó de maravilla. Es genial ver cómo se pueden aplicar esos conceptos en situaciones reales, y el artículo lo explica de una manera súper clara. ¡Gracias por compartir!