Teorema de Transferencia de Máxima Potencia: Prueba y Fórmula
En el fascinante mundo de la ingeniería eléctrica y la electrónica, el Teorema de Transferencia de Máxima Potencia se erige como un pilar fundamental para optimizar el rendimiento de los circuitos. Pero, ¿qué significa realmente este teorema y por qué es tan crucial en el diseño de sistemas eléctricos? En este artículo, exploraremos su principio básico, demostraremos su validez matemática y desglosaremos la fórmula que permite maximizar la eficiencia en la transferencias de energía. Si alguna vez te has preguntado cómo lograr que tus dispositivos funcionen a su máxima capacidad, sigue leyendo y descubre cómo aplicar este teorema puede transformar tus proyectos y conocimientos en el ámbito de la electrónica. ¡La potencia está a un clic de distancia!
Descubre el secreto detrás de la máxima potencia en tus circuitos eléctricos con el fascinante Teorema de Transferencia de Máxima Potencia. ¿Sabías que existe una fórmula infalible que te permitirá maximizar la eficiencia de tus sistemas? Aprende cómo poner a prueba este increíble teorema y aplícalo en tus proyectos para obtener resultados inigualables. ¡No te lo pierdas!
Teorema de transferencia de potencia máxima es una herramienta para determinar la condición de máxima transferencia de potencia. Teorema de transferencia de potencia máxima establece que la fuente puede entregar la máxima potencia a la carga si la resistencia de la carga es igual a la resistencia de la fuente. El teorema de máxima transferencia de potencia se aplica a los circuitos de CA y CC. Para obtener la máxima potencia de la fuente, la resistencia de la carga debe ser igual a la resistencia de la fuente. Derivaremos la prueba matemática del teorema de transferencia de potencia máxima y la eficiencia del sistema bajo transferencia de potencia máxima.
Explicación del Teorema de Transferencia de Potencia Máxima
En el caso de una fuente de CC, tiene cierta resistencia. En el caso de una fuente de CA, tiene cierta impedancia. La fuente alimenta corriente a la carga. La caída de voltaje tiene lugar en la impedancia de la fuente cuando la corriente fluye a través del circuito. La potencia perdida en la resistencia de la fuente debe ser mínima para obtener la máxima entrega de potencia de la fuente.
Si la pérdida de energía en la resistencia de la fuente es mayor, no se puede garantizar la entrega máxima de energía de la fuente. Existe cierta relación entre la impedancia de la fuente y la impedancia de la carga para la cual se puede lograr la máxima entrega de energía de la fuente. El teorema de la potencia máxima establece que si la resistencia de la carga es igual a la resistencia de la fuente, la fuente entregará la potencia máxima.
La resistencia de la fuente es la resistencia vista desde el lado de la carga, y podemos encontrar su valor usando el teorema de Thevenin. Por lo tanto, la resistencia de la fuente también se denomina resistencia de Thevenin. Tomamos el circuito de CC para comprender el teorema de transferencia de potencia máxima.
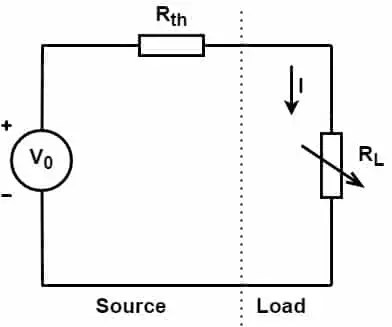
Circuito equivalente de Thevenins
>
En el circuito equivalente de Thevenin anterior, el teorema de transferencia de potencia máxima establece que «la cantidad máxima de potencia se entregará en la resistencia de carga si la resistencia de carga es igual a la resistencia de la fuente de Thevenin o Norton.
La resistencia de la fuente vista desde el lado de la carga es Rel y el voltaje de Thevenin es V0. Según el teorema de máxima transferencia de potencia, la máxima transferencia de potencia ocurre cuando la resistencia de la fuente es igual a la resistencia de la carga.
Rel = RL
Ejemplo de transferencia de potencia máxima: 1
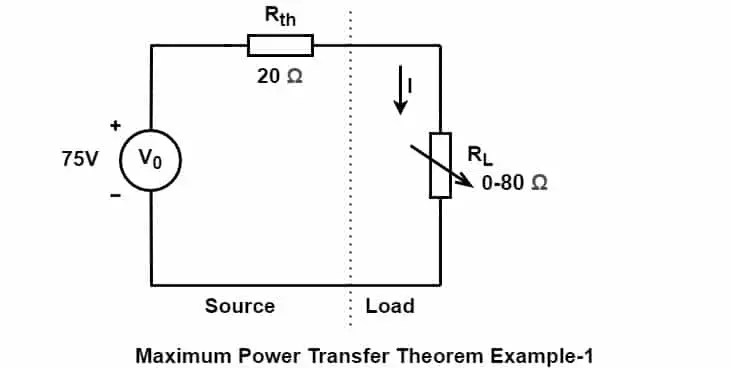
>De acuerdo con el teorema de transferencia de potencia máxima, la fuente entrega la potencia máxima a la carga si el valor de la resistencia de la carga es igual a la resistencia de la fuente. El valor de la resistencia de carga debe ser de 20 Ω. Ahora verifiquemos esta afirmación calculando la energía consumida por la carga en varias configuraciones de carga.
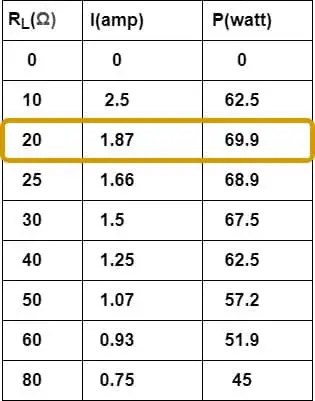
>Prueba del teorema de transferencia de máxima potencia
>
La máxima entrega de potencia es posible si;
>
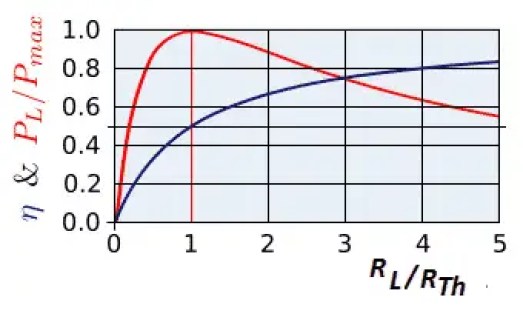
Por lo tanto, la condición para la transferencia de potencia máxima es la fuente que entrega la máxima potencia a la carga, si la resistencia de la fuente es igual a la resistencia de la carga. Ahora calcularemos el sistema. eficiencia en condiciones de máxima transferencia de potencia.
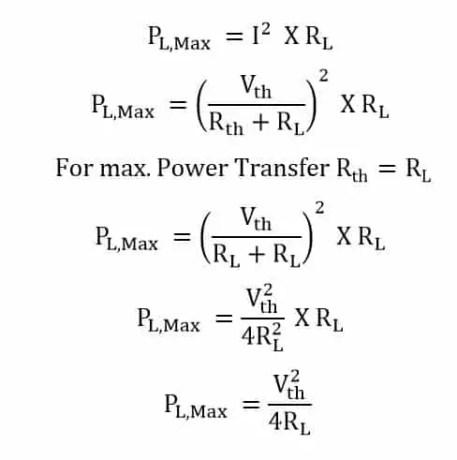
Eficiencia de la transferencia de potencia máxima
Potencia máxima entregada a la carga

>La potencia total transferida desde la fuente es:
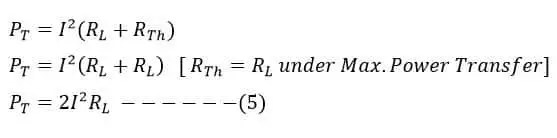
>
Podemos calcular la eficiencia máxima dividiendo la ecuación (4) y la ecuación (5)
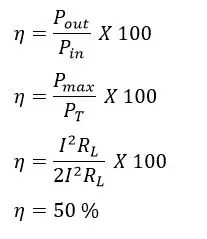
>Por lo tanto, en la condición de máxima transferencia de potencia, la eficiencia es del 50%. En condiciones de máxima transferencia de energía, la fuente entrega el 50 % de la energía generada a la carga y, en otras condiciones, la fuente conduce un pequeño porcentaje de energía a la carga.
>
Valor de resistencia de carga para transferencia de potencia máxima
>Aplicación del teorema de transferencia de máxima potencia
[automatic_youtube_gallery type=»search» search=»Teorema de transferencia de máxima potencia | Prueba, Fórmula» limit=»1″]
Teorema de Transferencia de Máxima Potencia
En el fascinante mundo de la ingeniería eléctrica y la electrónica, el Teorema de Transferencia de Máxima Potencia se erige como un pilar fundamental para optimizar el rendimiento de los circuitos.
¿Qué es el Teorema de Transferencia de Máxima Potencia?
El Teorema de Transferencia de Máxima Potencia establece que una fuente puede entregar su máxima potencia a una carga cuando la resistencia de la carga es igual a la resistencia de la fuente. Este teorema se aplica tanto a circuitos de corriente continua (CC) como a circuitos de corriente alterna (CA).
Principio del Teorema y Fórmula
Condición para la Máxima Transferencia de Potencia
La condición para lograr la máxima transferencia de potencia se puede expresar de la siguiente manera:
RL = Rf
donde RL es la resistencia de la carga y Rf es la resistencia de la fuente (también conocida como resistencia de Thevenin).
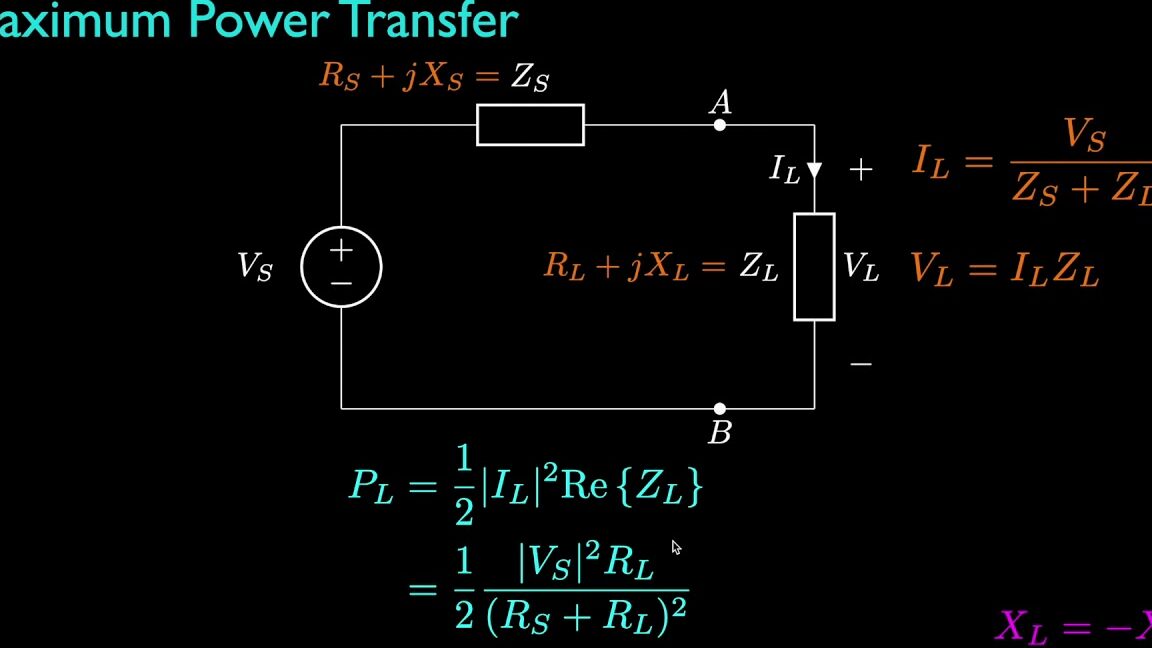
Demostración Matemática
Consideremos un circuito simple donde una fuente de potencia CC está conectada a una carga. La potencia entregada a la carga puede calcularse con la fórmula:
P = I² RL
Donde la corriente I puede ser expresada usando la ley de Ohm:
I = VS / (Rf + RL)
Al sustituir esta expresión en la fórmula de potencia se puede derivar que la entrega de potencia es máxima cuando la resistencia de carga es igual a la resistencia de la fuente. Para más detalle sobre la demostración, puedes consultar este recurso aquí[[2]].
Ejemplo de Aplicación
Supongamos que tenemos una resistencia de carga de 20 Ω. Para maximizar la potencia entregada, debemos asegurarnos de que la resistencia de la fuente también sea 20 Ω. Si realizamos la conexión adecuada, la potencia máxima que puede ser entregada a la carga se puede calcular directamente usando las fórmulas previamente mencionadas.
Preguntas Frecuentes (FAQs)
¿Qué sucede si la resistencia de la carga no es igual a la de la fuente?
Cuando la resistencia de la carga no coincide con la de la fuente, la potencia entregada es menor que la máxima posible. Esto resulta en pérdidas de eficiencia, ya que parte de la energía se disipa en la resistencia de la fuente.
¿El teorema se aplica a circuitos de CA?
Sí, el Teorema de Transferencia de Máxima Potencia también se aplica a circuitos de corriente alterna, tomando en cuenta la impedancia en lugar de la resistencia pura. Es crucial igualar la impedancia de carga con la impedancia de la fuente para maximizar la potencia transferida.
¿Cómo determinar la resistencia de Thevenin?
La resistencia de Thevenin se puede determinar al eliminar la carga del circuito y calcular la resistencia vista desde los terminales de la carga. Esto se realiza comúnmente usando el método de voltaje y corriente de circuito abierto.
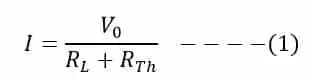

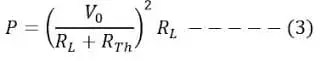
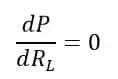
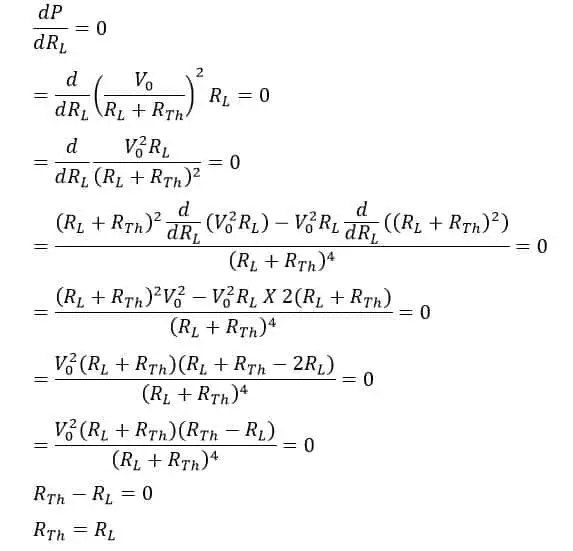
Jeico: ¡Totalmente de acuerdo, ziheng! A mí también me sorprendió cuando lo vi en clase. Una vez, en un laboratorio, intenté ajustar un sistema de audio y, al aplicar el teorema, pude mejorar la calidad del sonido de manera significativa. Es una locura cómo entender estas fórmulas puede marcar la diferencia en proyectos reales. ¡Me alegra leer que te pasó algo similar!
¡Me encanta el tema, ziheng! La verdad es que el teorema de transferencia de máxima potencia me voló la cabeza cuando lo estudié en la uni. Recuerdo que hice un proyecto para optimizar el rendimiento de un circuito y, al aplicar esta fórmula, ¡los resultados fueron increíbles! Es fascinante cómo algo tan teórico puede tener aplicaciones tan prácticas.
Marchesi: ¡Qué bueno leer sus experiencias! A mí me pasó algo parecido cuando estaba trabajando en un proyecto de robótica. Recuerdo que luchaba con la alimentación de mis motores y, al aplicar el teorema de transferencia de máxima potencia, logré que funcionaran mucho más eficientemente. Fue un alivio ver que, al final, todo encajaba. Definitivamente, es una fórmula que todos los que estamos en este rollo deberíamos tener fresca en la mente.