Puente de Desauty y Puente de Desauty Modificado: Diagrama de Circuito y Fasor
En el fascinante mundo de la ingeniería eléctrica, los circuitos de medición son claves para realizar análisis precisos y eficaces. Uno de los protagonistas en este campo es el Puente de Desauty, un dispositivo que, a pesar de su simplicidad, es capaz de revelar secretos fundamentales sobre la impedancia y otros parámetros eléctricos. En este artículo, adentrémonos en los entresijos de este puente original y su versión modificada. Exploraremos sus diagramas de circuito, analizaremos su funcionamiento mediante fasores y descubriremos las aplicaciones prácticas que revolucionan el estudio de la eléctrica moderna. ¡Preparemos las mentes curiosas para un viaje al corazón de la medición eléctrica!
Descubre el fascinante mundo de los puentes de Desauty y los puentes de Desauty modificados: acompáñanos en este artículo donde exploraremos en detalle su diagrama de circuito y el fenomenal concepto de fasor. Prepárate para adentrarte en el asombroso universo de la electrónica y descubrir cómo estos puentes revolucionaron el campo de los circuitos. ¡No te lo pierdas!
Puente de Desauty y Puente de Desauty modificado. se utilizan para encontrar el valor de la capacitancia desconocida. También se utilizan para comparar el valor de dos capacitancias.
El puente de Desauty es un tipo de puente de CA (corriente alterna) que se emplea para la medición de capacitancia desconocida. La principal ventaja del puente de Desauty es que brinda un alto grado de precisión en la medición de capacitancia en una amplia gama de capacitancias. Además, podemos utilizar el puente de De Sauty para comparar dos capacitancias.
Hay dos circuitos de construcción del Puente de Desauty, a saber:
- Puente de Sauty
- Puente de De Sauty modificado
Discutamos cada uno de estos dos puentes uno por uno.
Puente de Desauty
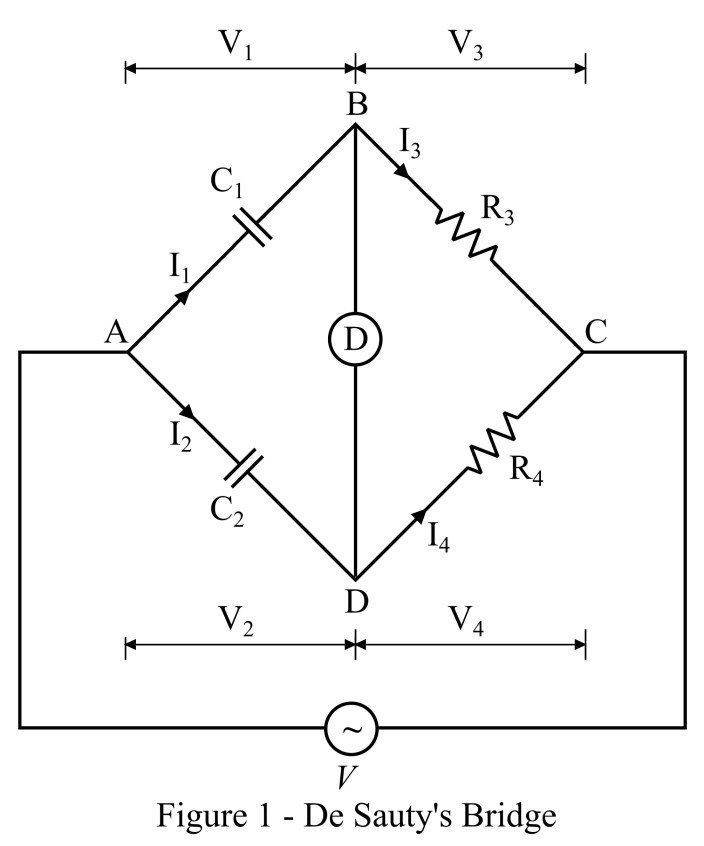
La construcción del circuito del puente de De Sauty se muestra en la Figura 1. Consta de cuatro brazos. Donde, el brazo AB tiene un capacitor, cuya capacitancia C1 se va a determinar. El brazo AD tiene un capacitor estándar conocido de capacitancia C2. Los brazos BC y CD tienen dos resistencias no inductivas estándar cuyas resistencias son R3 y R4 respectivamente. Una fuente de voltaje de CA está conectada a través de las terminales A y C.
El puente de Desauty se basa en el principio de deflexión nula, es decir, su condición de equilibrio se denota por la deflexión nula del inductor de deflexión nula, que está conectado entre los terminales B y D como se muestra en la figura 1.
 >Ahora, derivemos la expresión para el cálculo del valor de la capacitancia desconocida.
>Ahora, derivemos la expresión para el cálculo del valor de la capacitancia desconocida.
Del circuito del puente de Desauty, la impedancia de cada brazo del puente se da de la siguiente manera:
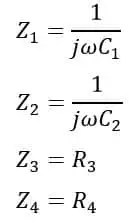 >
>
Se dice que el puente está equilibrado si
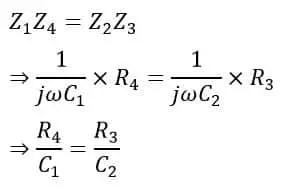 >Por lo tanto, el valor de la capacitancia desconocida se puede determinar usando la siguiente fórmula,
>Por lo tanto, el valor de la capacitancia desconocida se puede determinar usando la siguiente fórmula,
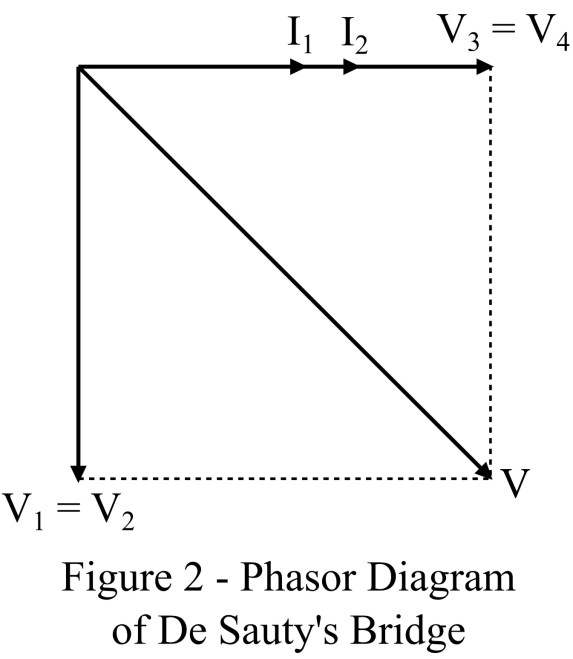
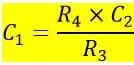 >La ventaja más significativa del puente de De Sauty es su construcción de circuito simple y solo componente variable. Donde podemos seleccionar cualquiera de las resistencias R3 o R4 como un componente variable para llevar el puente a una condición de equilibrio. El diagrama fasorial del puente de Desauty se muestra en la Figura 2.
>La ventaja más significativa del puente de De Sauty es su construcción de circuito simple y solo componente variable. Donde podemos seleccionar cualquiera de las resistencias R3 o R4 como un componente variable para llevar el puente a una condición de equilibrio. El diagrama fasorial del puente de Desauty se muestra en la Figura 2.
 >Ahora, analicemos el puente de De Sauty modificado, la construcción de su circuito y el diagrama fasorial.
>Ahora, analicemos el puente de De Sauty modificado, la construcción de su circuito y el diagrama fasorial.
Puente de Desauty modificado
El puente de Desauty modificado es una versión mejorada del puente de Desauty básico. Está diseñado para medir la capacitancia desconocida de un capacitor imperfecto. Donde, un capacitor imperfecto, también llamado un condensador con pérdidases aquel que tiene una resistencia interna finita debido a las pérdidas dieléctricas.
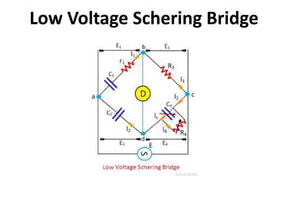
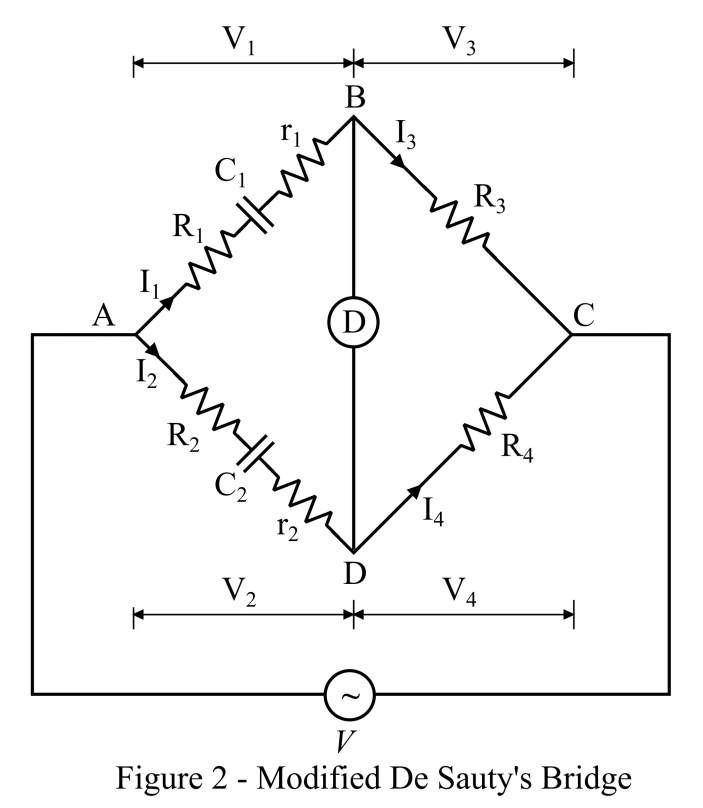 >La construcción del circuito del puente de Desauty modificado se muestra en la Figura 3. El puente de Desauty modificado consta de cuatro brazos, a saber, AB, AD, BC y CD. El brazo AB tiene una resistencia R1 conectado en serie con un capacitor desconocido imperfecto cuya capacitancia es C1 y la resistencia interna es r1. El brazo AD tiene una resistencia R2 conectado en serie con un capacitor imperfecto cuya capacitancia es C2 y la resistencia interna es r2. Los brazos BC y CD tienen resistencias no inductivas cuyas resistencias son R3 y R4 respectivamente.
>La construcción del circuito del puente de Desauty modificado se muestra en la Figura 3. El puente de Desauty modificado consta de cuatro brazos, a saber, AB, AD, BC y CD. El brazo AB tiene una resistencia R1 conectado en serie con un capacitor desconocido imperfecto cuya capacitancia es C1 y la resistencia interna es r1. El brazo AD tiene una resistencia R2 conectado en serie con un capacitor imperfecto cuya capacitancia es C2 y la resistencia interna es r2. Los brazos BC y CD tienen resistencias no inductivas cuyas resistencias son R3 y R4 respectivamente.
Ahora, derivemos la expresión para el cálculo de la capacitancia desconocida del capacitor C1.
Del diagrama de circuito del puente de Desauty modificado, las impedancias de los brazos del puente son,
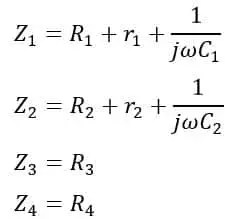 >
>
Para que el puente esté en condiciones de equilibrio,
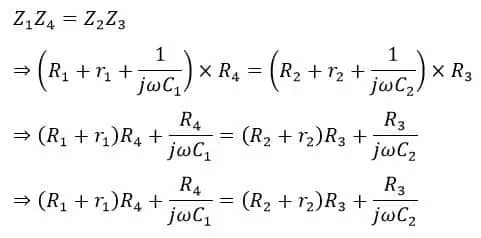 >Al igualar los términos reales de la ecuación en ambos lados, tenemos,
>Al igualar los términos reales de la ecuación en ambos lados, tenemos,
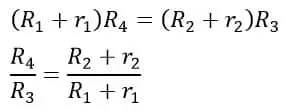 >Al igualar términos imaginarios en ambos lados, tenemos,
>Al igualar términos imaginarios en ambos lados, tenemos,
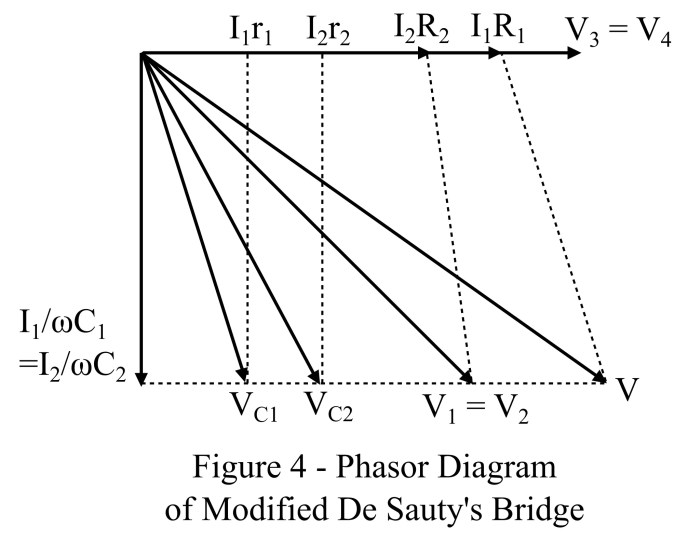
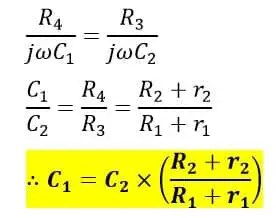 >Por lo tanto, podemos calcular el valor de la capacitancia desconocida C1 utilizando esta fórmula. El diagrama fasorial del puente de De Sauty modificado se muestra en la Figura 4.
>Por lo tanto, podemos calcular el valor de la capacitancia desconocida C1 utilizando esta fórmula. El diagrama fasorial del puente de De Sauty modificado se muestra en la Figura 4.
 >Por lo tanto, se trata de la construcción y la teoría del puente de Desauty y el puente de Desauty modificado. Como comentamos, los puentes de Desauty se utilizan para medir la capacitancia desconocida en un circuito de CA.
>Por lo tanto, se trata de la construcción y la teoría del puente de Desauty y el puente de Desauty modificado. Como comentamos, los puentes de Desauty se utilizan para medir la capacitancia desconocida en un circuito de CA.
[automatic_youtube_gallery type=»search» search=»Puente de Desauty y puente de Desauty modificado: diagrama de circuito y fasor» limit=»1″]
Puente de Desauty y Puente de Desauty Modificado: Diagrama de Circuito y Fasor
En el fascinante mundo de la ingeniería eléctrica, los circuitos de medición son claves para realizar análisis precisos y eficaces. Uno de los protagonistas en este campo es el Puente de Desauty, un dispositivo que, a pesar de su simplicidad, revela secretos fundamentales sobre la impedancia y otros parámetros eléctricos. En este artículo, adentrémonos en los entresijos de este puente original y su versión modificada.
¿Qué es el Puente de Desauty?
El Puente de Desauty es un dispositivo utilizado para la medición precisa de capacitancia desconocida, ideal para aplicaciones que requieren alta fidelidad en los resultados. Se basa en una técnica de balance, donde la condición de equilibrio se logra cuando la deflexión de un instrumento de medición es nula.
Componentes del Puente de Desauty
- Capacitor Desconocido (C1): El componente cuya capacitancia se desea medir.
- Capacitor Patrón (C2): Un capacitor de capacitancia conocida que sirve como referencia.
- Resistencias (R3 y R4): Resistencias estándar utilizadas para el ajuste del puente.
- Fuente de Voltaje de CA: Proporciona la tensión necesaria para el funcionamiento del circuito.
Diagrama de Circuito
El diagrama de circuito del Puente de Desauty se puede observar en diversas referencias. Este circuito consta de cuatro brazos que interconectan los componentes mencionados, facilitando el balance adecuado entre la impedancia de los brazos de medición.
¿Cómo Funciona el Puente de Desauty?
Para que el puente esté equilibrado, se requiere ajustar las resistencias y capacitores hasta alcanzar la condición de deflexión nula. Se puede derivar la expresión para la capacitancia desconocida usando las relaciones de impedancia en cada brazo del puente:
C1 / C2 = R3 / R4
De esta manera, al ajustar las resistencias, es posible determinar la capacitancia desconocida (C1) con alta precisión.
Puente de Desauty Modificado
El Puente de Desauty modificado es una versión mejorada que permite medir capacitores imperfectos, aumentando la versatilidad y las aplicaciones del dispositivo. Este puente incluye ajustes adicionales para mejorar la precisión en condiciones variables y ofrece un enfoque eficiente para mediciones más complicadas.
Mejoras en el Diseño
- Mejora en la linealidad de medición.
- Mayor capacidad para manejar errores de medición.
- Facilidad en el ajuste y calibración.
Así, el puente modificado se convierte en una opción atractiva para laboratorios y aplicaciones industriales donde la precisión y la adaptabilidad son esenciales.
Diagramas de Fasores
El análisis del comportamiento del Puente de Desauty a través de diagramas de fasores proporciona una representación visual de cómo las señales de voltaje y corriente interactúan en el circuito. Esto es especialmente útil para comprender la fase entre las diferentes impedancias debido a la presencia de componentes reactivos.
Preguntas Frecuentes (FAQs)
¿Cuáles son las aplicaciones del Puente de Desauty?
El Puente de Desauty se utiliza principalmente en laboratorios de investigación, educación técnica y en la industria para medir capacitancias desconocidas y realizar comparaciones precisas entre capacitores.
¿Qué ventajas tiene el uso de un puente modificado?
El puente de Desauty modificado presenta mejoras en la precisión de medición, adaptabilidad para capacitores de calidad variable y una interfaz de usuario simplificada para facilitar los ajustes necesarios.
¿Cómo se calibra el Puente de Desauty?
La calibración implica el uso de un capacitor de referencia conocido y el ajuste de las resistencias hasta alcanzar el equilibrio, lo que se puede verificar mediante la deflexión nula en el medidor asociado.
Conclusión
El Puente de Desauty y su versión modificada son herramientas esenciales en la medición eléctrica, proporcionando un alto grado de precisión y versatilidad en diversas aplicaciones. Su diseño simple pero efectivo ha dejado una marca significativa en el campo de la ingeniería eléctrica, y su comprensión es crucial para profesionales en esta área.
Para más información sobre otros dispositivos de medición, puedes visitar el siguiente recurso: PPT sobre puentes de medida.